You can see that it’s limited by the materials in the tires and track (captured by the frictional coefficent) and the gravitational field (so, what planet you’re on). Notice that the mass has canceled out. It doesn’t matter if you have a more massive vehicle. Yes, you get more friction, but it’s also harder to accelerate.
Constant-Friction Model
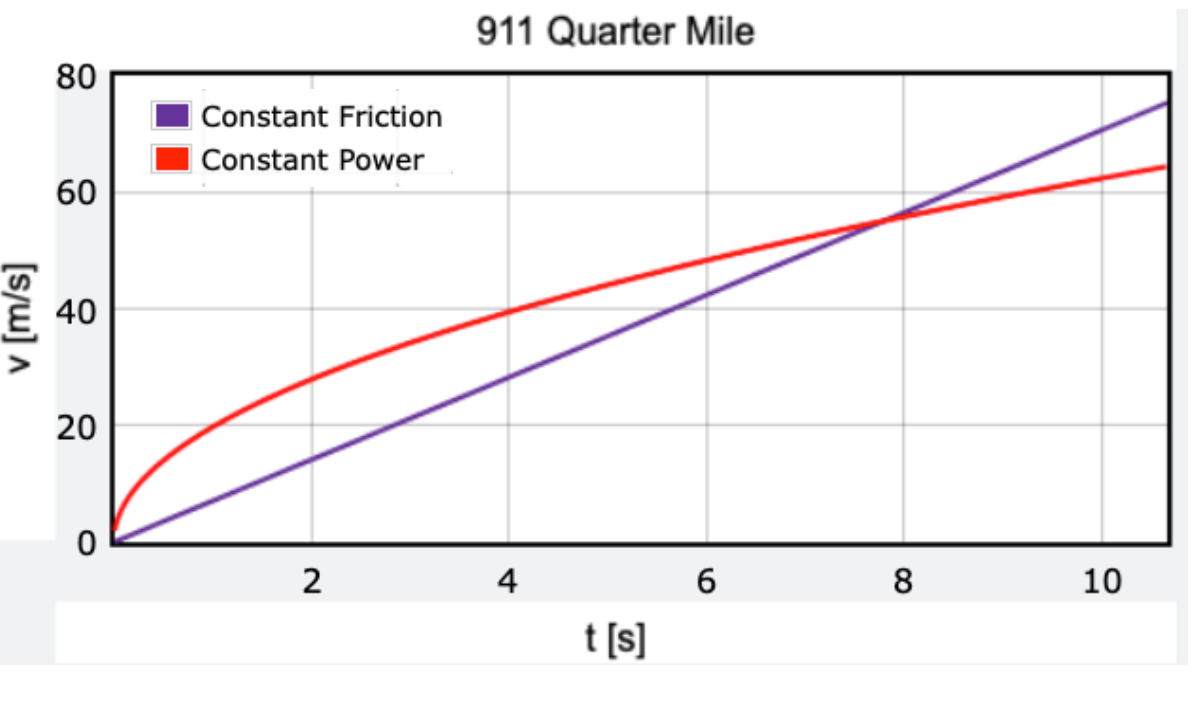
Since constant power doesn’t work, what about a constant acceleration due to the friction between the tires and road? Let’s say the coefficient of friction is 0.7 (reasonable for a dry road). In that case we would get the following plot of velocity versus time for the quarter-mile run.
I’ve included the constant-power curve just for comparison. You can see that with this friction model, the car will just keep increasing in speed forever with the same acceleration. That doesn’t seem correct either.
A Better Model of Acceleration
How about this? The car increases in velocity—however, the rate of increase (the acceleration) is the lower of the two models. So, at the beginning of the run the acceleration is limited by the friction between the tires and road. Then, when the acceleration using the constant power model is lower, we can use that method.
Before we test this out, we need some real data for comparison. Since I don’t own a Porsche 911, I’m going to use the data from this MotorTrend race between a 911 and a Tesla Cybertruck. Here is a plot of the actual position of the Porsche over the quarter-mile track along with the combo power-friction model. (That’s now distance on the vertical axis—a quarter-mile is just about 400 meters.)